近期,课题组硕士生洪钰淞(导师:叶蔚副教授)在 Building and Environment(Q1,IF:7.6)上发表了基于高斯过程回归的受限空间中移动热源定位研究。该研究探讨了在低可视度和复杂气流条件下,通过温度场反演实现移动热源定位的可行性。构建了包含多种热源强度、运动轨迹及通风条件的计算流体动力学(CFD)数值模型,并搭建实验平台获取对比数据。利用高斯过程回归(GPR)方法建立了温度分布与热源位置的映射模型,对比了四种核在预测性能上的差异。结合支持向量回归(SVR)、随机森林(RF)和人工神经网络(ANN)模型进行误差分析。进一步采用最小冗余最大相关(mRMR)算法进行传感器布置优化,在仅保留6个关键传感器的条件下,定位误差保持在0.2 m以内。最后通过引入高斯噪声与传感器漂移误差,评估了模型的鲁棒性与误差敏感性。

原文链接:
https://doi.org/10.1016/j.buildenv.2025.113909
研究背景:
在隧道、地下矿井及工业车间等受限空间中,热源位置的快速识别与跟踪对于环境调控、安全防护和故障预警具有重要意义。此类空间通常封闭且气流条件复杂,热源分布呈现高度非均匀性与动态性。传统的热源监测多依赖视觉或红外成像手段,但在烟雾、蒸汽或遮挡等低可视度环境中,这些方法的识别精度与连续性显著下降。此外,基于单点测温的经验方法只能提供局部温度变化,难以反映整体温度场特征,导致热源定位精度不足。为实现更高分辨率的热源识别,研究者尝试利用计算流体动力学(CFD)方法重建三维温度场分布,但此类方法计算代价高、对边界条件依赖强,难以满足实时定位的需求。
针对上述问题,已有研究提出通过数据驱动的方式利用温度传感网络进行热源反演,但相关工作多局限于静态或稳态工况,对热源运动、流场扰动及测点稀疏条件下的动态定位研究仍较少。特别是在受限空间中,热源位置的变化会引起气流结构重构和温度梯度反转,使得传统算法的稳定性和泛化能力受限。为弥补现有研究的不足,本研究提出了一种基于高斯过程回归(GPR)的非视觉热源定位方法,旨在利用温度场信号反演热源位置,实现受限空间内的动态精确定位。通过数值模拟与实尺度实验结合,系统验证了模型的预测精度与稳定性,并探讨了传感器布置、噪声扰动及核函数结构对定位性能的影响。大型科学设施是国家科技创新体系的核心基础设施,其运行需依赖超高精度的恒温环境。传统恒温室通常采用垂直单向气流设计,通过顶部/底部静压箱实现
本研究的主要创新包括:1)构建考虑热源运动与气流耦合的动态CFD仿真模型,生成多工况温度数据集;2)利用GPR建立温度分布与热源位置的映射模型,并系统比较不同核函数的预测性能;3)通过最小冗余最大相关(mRMR)算法优化传感器布置,实现稀疏测点下的高精度预测;4)引入高斯噪声与传感器漂移误差开展鲁棒性分析,评估模型在复杂环境中的稳定性。研究成果为受限空间热源定位提供了系统的建模与验证路径,为隧道及地下空间热环境监测提供可推广的技术基础。
研究结论:
本研究分析并探讨了如何基于高斯过程回归(GPR)实现受限空间内移动热源的动态定位。首先,研究通过计算流体动力学(CFD)方法建立了包含多种热强度、运动轨迹及气流条件的动态温度场模型,生成大规模仿真数据集用于模型训练与对比。其次,搭建了实验平台,布设顶部与侧墙两类传感阵列,在不同热源运动速度与环境扰动下采集实验数据,以验证模型的预测能力与稳定性。第三,基于仿真与实验数据,构建GPR定位模型并系统比较了多种核函数(平方指数核、指数核、Matérn 5/2核、二次有理核)的预测性能;同时与支持向量回归(SVR)、随机森林(RF)及人工神经网络(ANN)等典型机器学习方法进行对比分析。研究进一步采用最小冗余最大相关(mRMR)算法进行传感器重要性排序与布置优化,在减少测点数量的同时保持高定位精度。最后,通过引入高斯噪声与传感器漂移误差,评估了模型在测量扰动与长期偏差条件下的鲁棒性,并探讨其在实际部署中的适用性。主要研究发现如下:
1. GPR模型在不同工况下均实现了高精度定位,模拟与实验平均误差分别为0.027 m与0.055 m,显著优于SVR、RF及ANN模型。
2. Matérn 5/2核在精度与计算效率之间取得最佳平衡,超参数分析确定了稳定预测的参数范围,为模型部署提供参考。
3. 经mRMR算法筛选,仅6个关键传感器即可保持约0.05 m的误差水平,实现了布点简化与性能均衡。
4. 在随机噪声幅度小于±0.8 °C时,模型误差稳定控制在0.2 m以内;当噪声进一步增大或传感器出现±1.5 °C以上系统漂移时,定位误差迅速上升;在漂移达到±5 °C时,误差增长至约1 m。
部分图示:
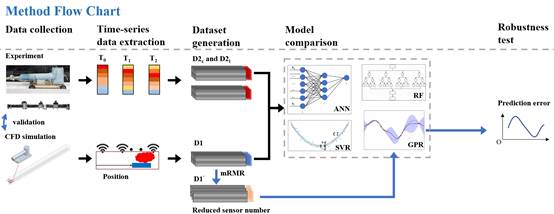
图1.研究框架
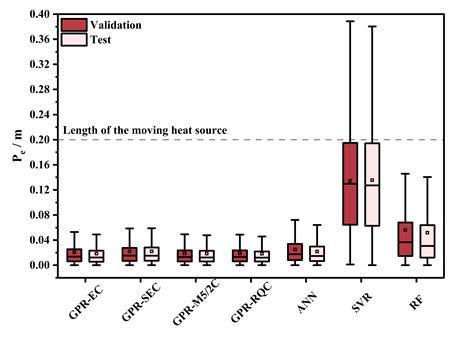
(a) 基于模拟数据集的训练结果
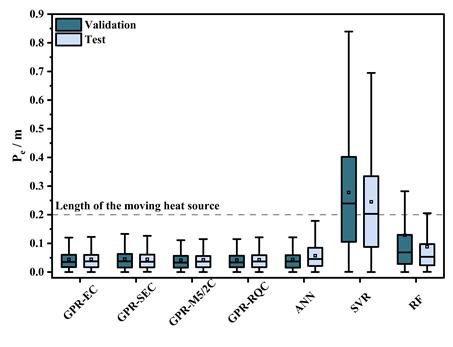
(b) 基于实验顶部测点数据集的训练结果
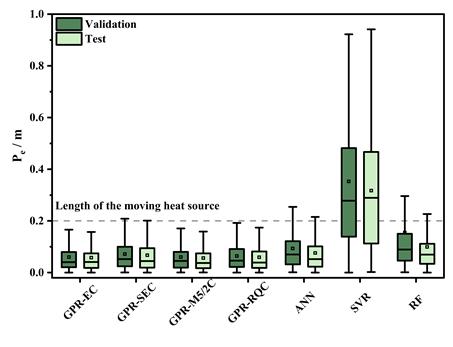
(c) 基于实验侧面测点数据集的训练结果
图2.基于不同数据集的算法预测偏差对比
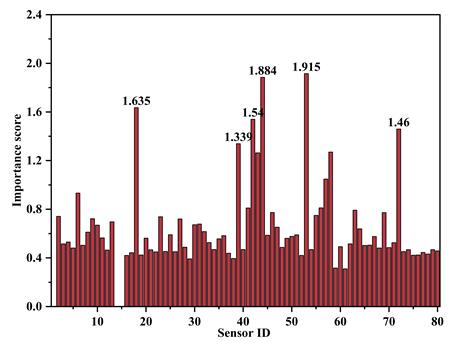
(a) 基于模拟数据集的结果
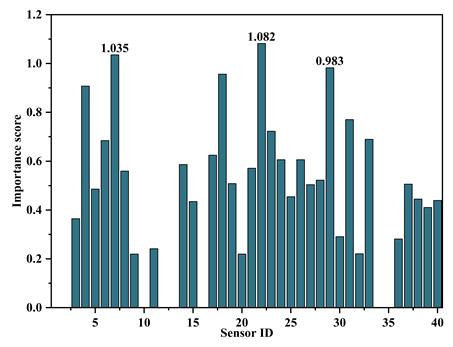
(b) 基于实验顶部测点数据集的结果
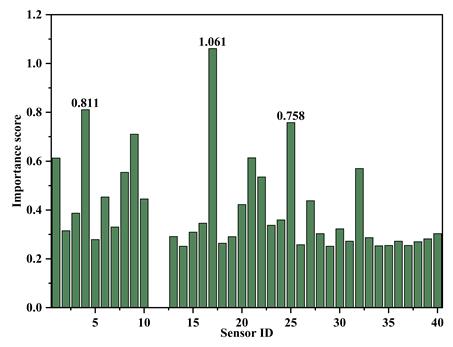
(c) 基于实验侧面测点数据集的结果
图3.基于mRMR算法对三个数据集的传感器重要性排序结果
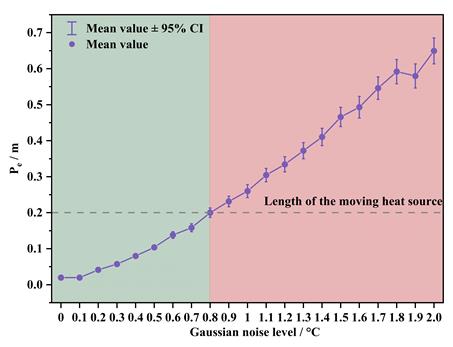
(a) 低高斯噪声条件下的定位误差分析
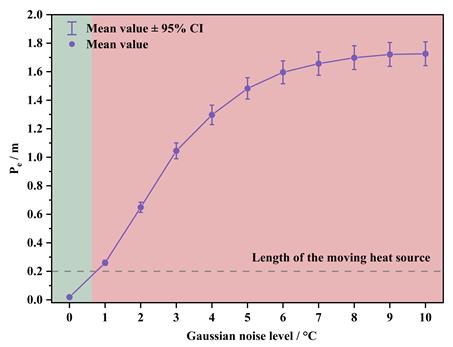
(b) 高高斯噪声条件下的定位误差分析
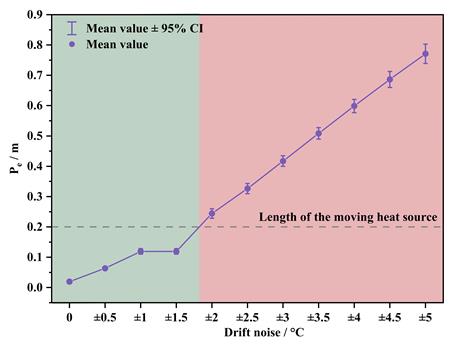
(c) 系统性传感器漂移下的定位误差分析
图4.不同噪声强度下预测误差对比
Copyright@ 同济大学张旭教授课题组

 同济大学主页
同济大学主页